Understanding Binary Heaps (MinHeap and MaxHeap) in JavaScript
In this series we’re going to explore some must-know data structures as visually and engaging as possible. This post will hopefully help you to understand binary heaps - more specifically, MinHeap and MaxHeap.
Why?
MinHeaps and MaxHeaps are useful when you need quick access to the smallest (for MinHeap) or largest (for MaxHeap) element in a long list of elements. MinHeaps are often the data structure of choice for Priority Queues. Several other use-cases include:
- Sorting (using Heap Sort)
- Various Selection Algorithms
- Graph Algorithms (Dijkstra’s Algorithm for example)
- Passing Interviews 😄
Binary Heaps and Binary Trees
A MinHeap or MaxHeap is mostly implemented as a Binary Heap. This means that (like a Binary Tree), all tree nodes have at most 2 children.
Additionally, a Binary Heap should always be a “complete binary tree”. Later in the article we’ll understand why this is the case. Let us first understand what a complete binary tree means.
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
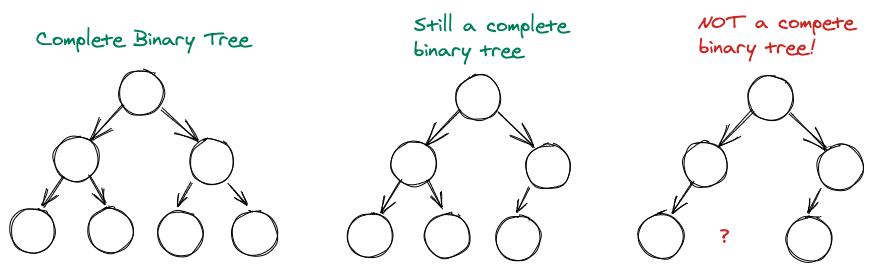
Complete Binary Trees
As you can see, the first tree is a complete binary tree because each level is completely filled. The second tree is still a complete binary tree due to every level being filled except the last, where all nodes are as left as possible.
The third tree is missing a right leaf node and can not be considered a complete binary tree.
MinHeap or MaxHeap
In this article we are going to implement a MinHeap. You will often see MinHeap and MaxHeap in the same article / video / context. This is because they are extremely similar with one key difference.
For a MinHeap, the node at the root of the tree must be the minimum value’s node in the whole tree. This needs to recursively true across the entire tree.
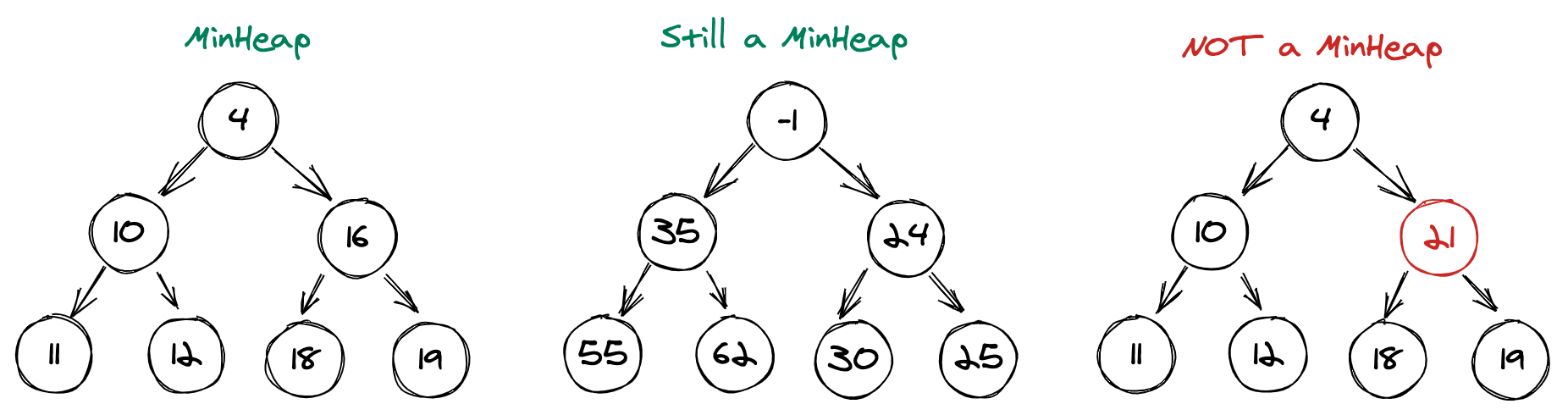
2 MinHeaps and 1 Binary Tree (because 21 is larger than 18 and 19)
Left and right children don’t have to be in perfect order for it to be a MinHeap. As long as the root (or parent node) is larger than its children.
Now for a MaxHeap, the node at the root of the tree must be the maximum value’s node in the whole tree. This needs to recursively true across the entire tree.
For the rest of the article, we’ll be working on a MinHeap. Once you understand a MinHeap, you’ll be able to create a MaxHeap with ease.
Creating our MinHeap
Because a MinHeap is a complete binary tree, it’s the perfect candidate to have its values stored into an array.
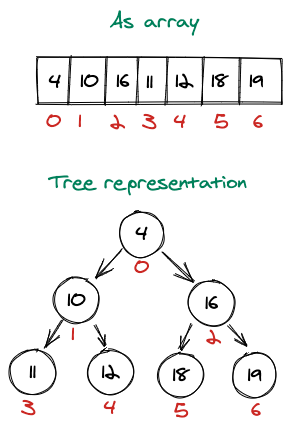
MinHeap stored as Array, displayed as Binary Tree
With this structure, starting from the index of a given node, we can easily navigate to child and parent nodes.
- Parent:
parentIndex = Math.floor((nodeIndex - 1) / 2); - Left child:
leftIndex = 2 * nodeIndex + 1; - Right child:
rightIndex = 2 * nodeIndex + 2;orleftIndex + 1;
For the parent we call Math.floor in case the index is an even number. If we didn’t floor we would be looking at index (10 - 1) / 2 = 4.5, this is obviously wrong.
The + 1 and -1 you see in those formulas are just because arrays are 0 based! They start at 0 instead of 1. Because the amount of leaf nodes doubles each time, we multiply to get the children. Therefore, we only need to divide to get the parent.
Here is how simple it would be if arrays started at 1:
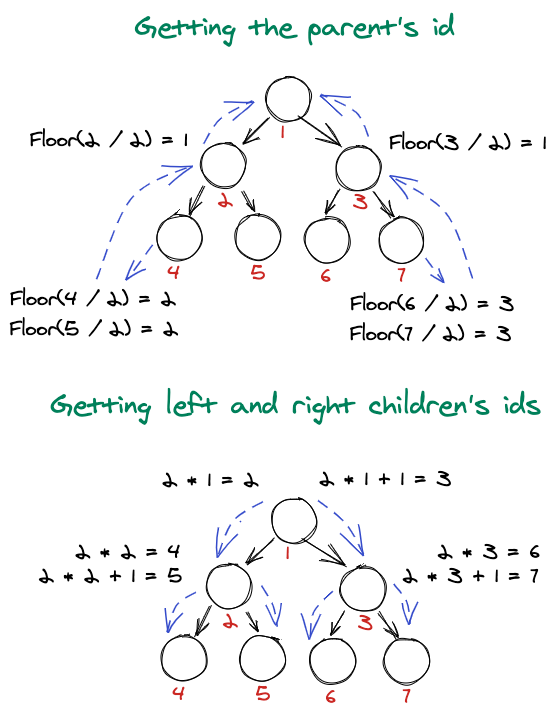
If arrays weren’t 0 based
Let’s implement our MinHeap using a JavaScript.
class HeapNode { constructor(importance, content) { if (typeof importance !== 'number') { throw new Error('Expected importance to be a number!'); } this.importance = importance; this.content = content; }}
class Heap { // Array representation of our Heap, see image above _elements = [];
get size() { return this._elements.length; }
push(heapNode) { /* we'll get there */ } pop() { /* keep on reading */ }
getParentIndex(nodeIndex) { // The root node does not have a parent if (nodeIndex === 0) return null;
return Math.floor((nodeIndex - 1) / 2); }
getChildrenIndices(nodeIndex) { const leftIndex = nodeIndex * 2 + 1; const rightIndex = leftIndex + 1;
// Children will be [null, null] if called on leaf nodes return [leftIndex, rightIndex].map(index => index < this.size ? index : null); }}Alright, that’s a good start. We have our base for our MinHeap. In getChildrenIndices you can see a freaky .map that checks if the indices are smaller than the heap size. This because if we were to calculate the children of any of the leaf nodes (nodes completely at the bottom of the tree). Their indices would not point actual nodes in the tree.
Adding (pushing) to our MinHeap
The way we insert new elements into our MinHeap follows a pretty simple algorithm:
- Add the new node to the end of our complete binary tree (the last array item in our implementation).
- Compare the node’s value with its parent’s value. If it’s larger, then we are done.
- If it’s smaller swap the two. Recursively do so on the (new) parent until we reach the root or the previous condition doesn’t match.
Before we write any code, let’s just look this it visually.
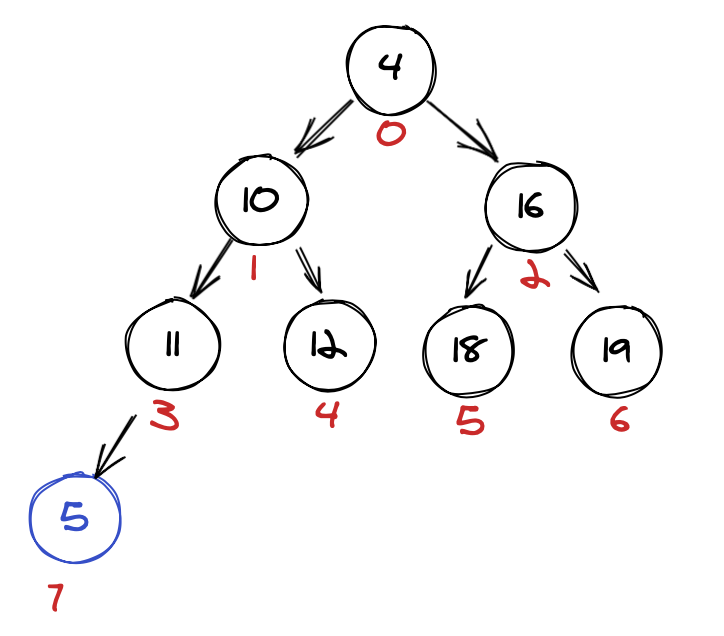
Add (5) to our MinHeap
We add 5 to our MinHeap. Let’s follow the algorithm. Is 5 smaller than its parent 11? yes! Swap them and recursively continue.
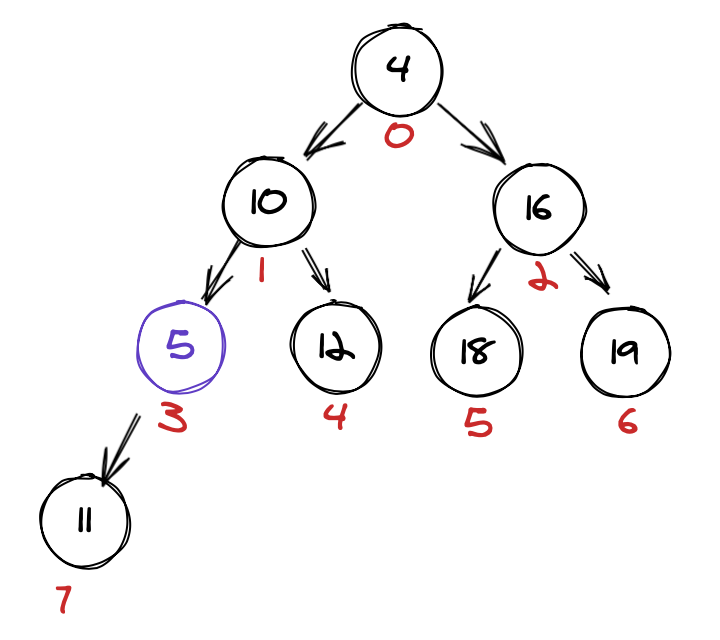
(5) moved up
Is 5 smaller than 10? Yes! Swap them and recursively continue.
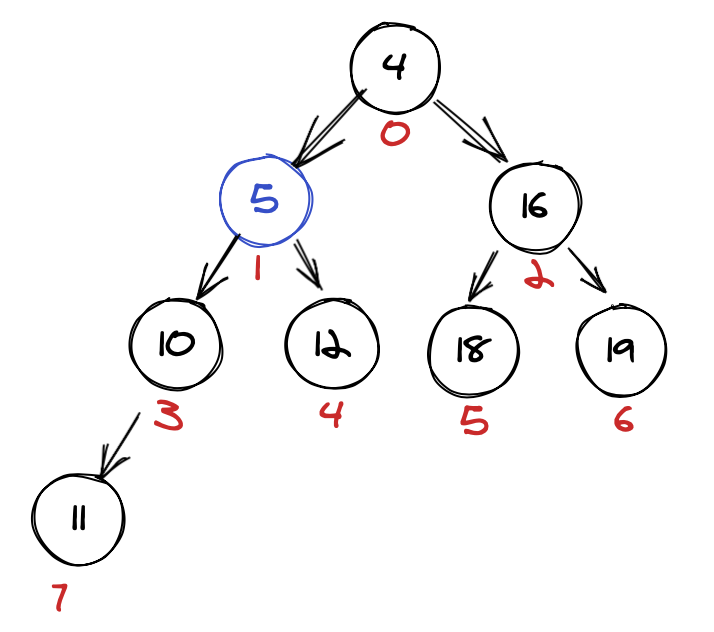
(5) moved up again
Is 5 smaller than 4? No! We’re done!
That wasn’t so bad, was it? Let’s implement it!
class MinHeap { _elements = []; ... push(heapNode) { this._elements.push(heapNode); this.moveUp(this.size - 1); }
moveUp(nodeIndex) { const parentIndex = this.getParentIndex(nodeIndex);
if (parentIndex === null) { // We reached the root node return; }
const currentNode = this._elements[nodeIndex]; const parentNode = this._elements[parentIndex];
if (currentNode.importance < parentNode.importance) { this.swap(nodeIndex, parentIndex); // Recursively do so this.moveUp(parentIndex); } }
swap(indexOne, indexTwo) { /* you got this */ }}We now have a working MinHeap! You can’t remove (or pop) any items from it yet.. but you could totally throw a ton of numbers at it, and it would always have the smallest item at the top!
Removing (popping) from our MinHeap
Removing (or popping) the first element from our MinHeap is a bit more complex than adding to it. First we’ll describe the algorithm. Then we’ll visually walk through it, and finally we’ll implement it.
The algorithm is as follows:
- Store the root node (minimum value) of our MinHeap
- Swap the last node (the rightmost leaf node at the last level) with the root node
- Compare the new root node with its children and swap it with the smallest child
- Recursively do so until you reach the bottom of the tree or the previous condition doesn’t match
It’s a bit more complicated but still nothing to be afraid of! Let’s see it in action.
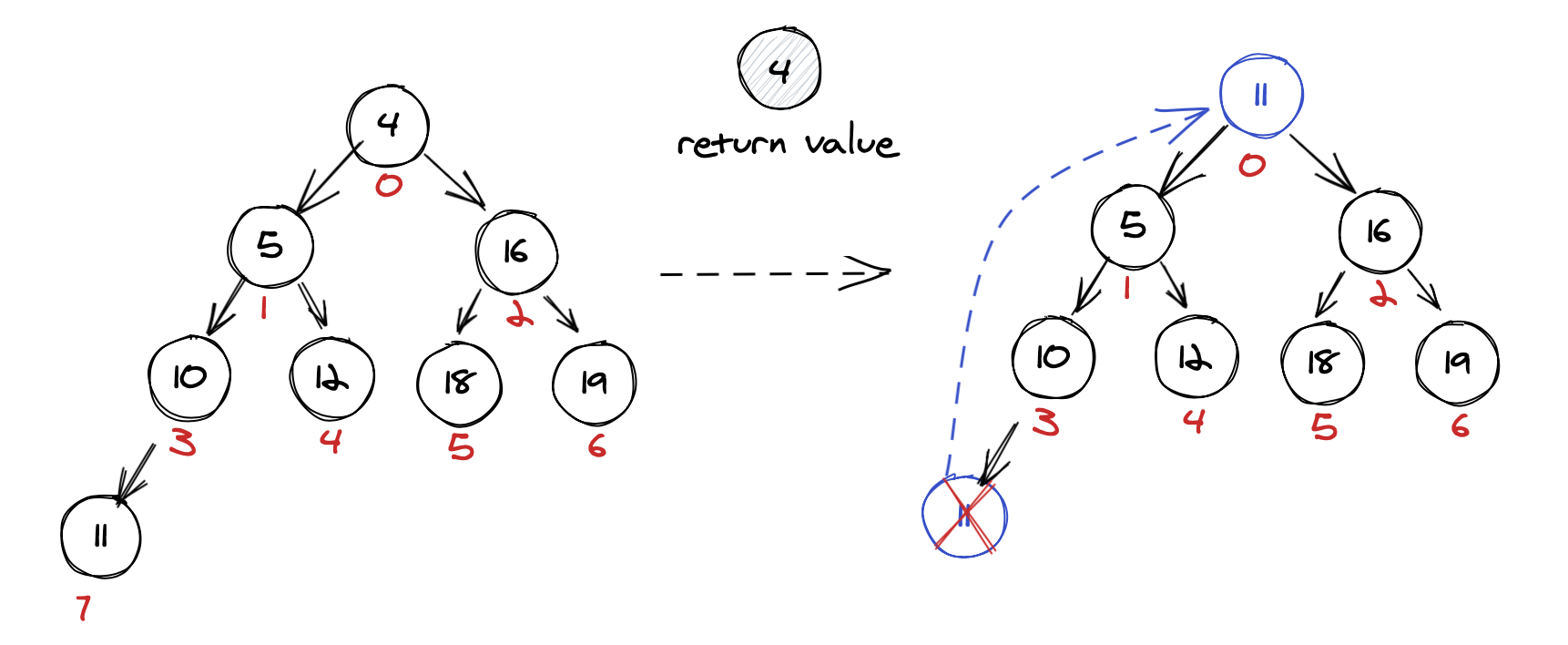
Remove the root node and replace it with the last node
We’ve moved the last element to the root. Danger! The root is now not the smallest value in the MinHeap… so it’s not a MinHeap! Time to follow the rest of the algorithm and swap nodes until we’re good again.
Is 11 larger than 5? Yes! Is 11 larger than 16? No. Swap 5 and 11.
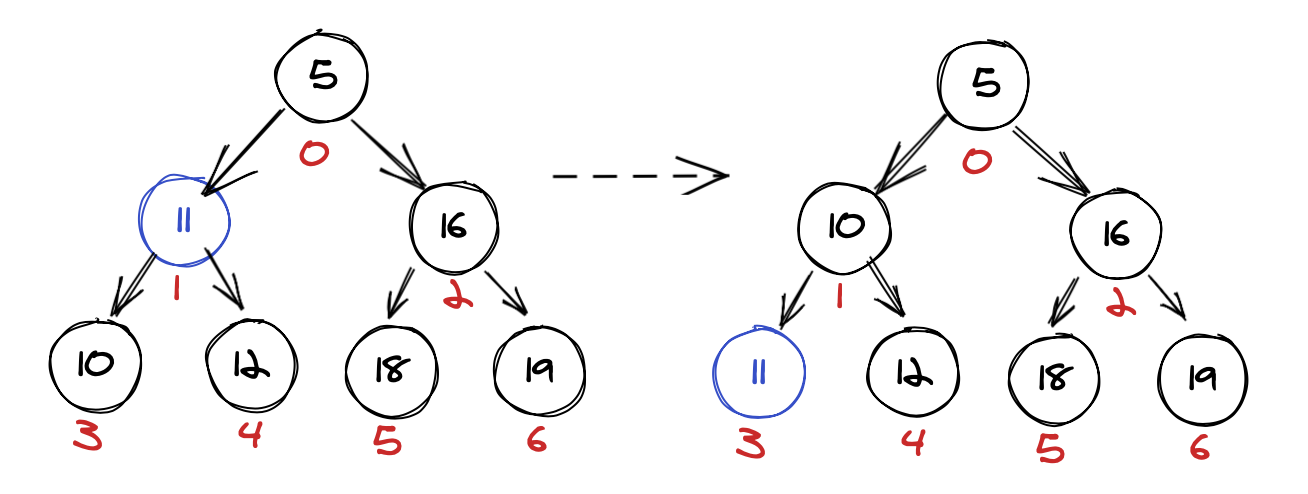
Is 11 larger than 10? Yes! Is 11 larger than 12? No. Swap 10 and 11.
Woah! We’ve now popped the minimum value from our MinHeap and restored it. Let’s see one more example as to why it is important to always swap with the smallest child.
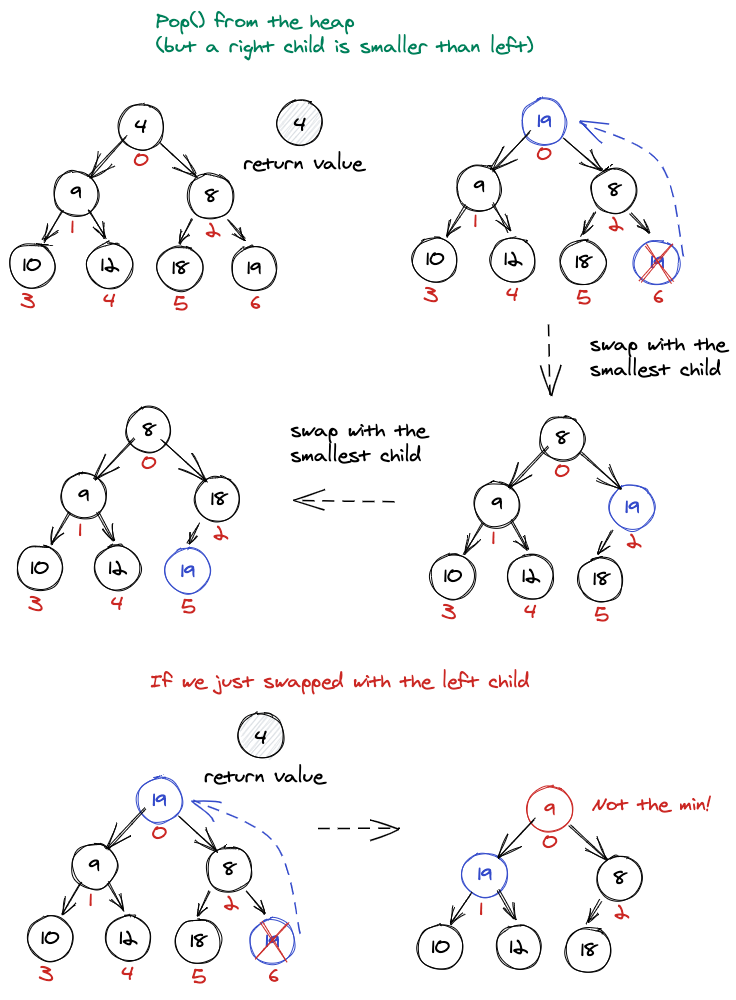
It’s important to swap with the smallest child
Perfect. Now that we’ve seen it in action, it is much easier to write the code.
class MinHeap { _elements = []; ... push(heapNode) {...} moveUp(nodeIndex) {...}
pop() { const node = this._elements[0]; const lastNode = this._elements.pop();
if (this._elements.length) { this._elements[0] = lastNode; this.moveDown(0); }
return node; }
moveDown(nodeIndex) { const [leftIndex, rightIndex] = this.getChildrenIndices(nodeIndex);
if (leftIndex === null) { // Because there is no leftIndex, there will also be no rightIndex and this means // we are at a leaf (a final node of the binary tree) return; }
let swapIndex = null; const parentNode = this._elements[nodeIndex]; const leftChild = this._elements[leftIndex]; if (leftChild.importance < parentNode.importance) { swapIndex = leftIndex; }
if (rightIndex !== null) { const rightChild = this._elements[rightIndex]; if (swapIndex !== null) { if (rightChild.importance < leftChild.importance) { swapIndex = rightIndex; } } }
if (swapIndex === null) { // No swapping is necessary, we've moved all the way down return; }
this.swap(nodeIndex, swapIndex)
// Recursively apply this function this.moveDown(swapIndex); }
swap(indexOne, indexTwo) {...}}That’s it! This is a fully working MinHeap. Pretty cool right? 🔥
const heap = new Heap();heap.push(new HeapNode(10, 'Go shopping'));heap.push(new HeapNode(20, 'Wash dishes'));heap.push(new HeapNode(1, 'Write blogpost'));let currentTask = heap.pop(); // Write blogpostheap.push(new HeapNode(420, 'Buy vegetables'));currentTask = heap.pop(); // Go shoppingSolidify your understanding
The best way to solidify your understanding is to put what you’ve just learned into practice. Here are 2 exercises you could do if you feel like it:
- Implement a MaxHeap
- Implement a remove method (similar to pop, but for any node in the tree)